Analysis = Infinitesimalrechnung » Die e-Funktion und ihre Umkehrfunktion die ln-Funktion » Das Wichtigste zur ln-Funktion » Einführung des natürlichen Logarithmus, kurz ln » Die ln-Funktion spiegeln, stauchen/strecken und verschieben

Die ln-Funktion spiegeln, stauchen/strecken und verschieben

Auch auf folgendem Weg ergibt sich der Graph von :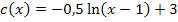

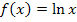
Verschiebung von 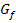um 1 nach rechts

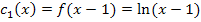
Spiegelung von an der x-Achse

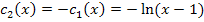
Stauchung von 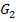entlang der y-Achse mit dem Faktor 0,5

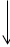
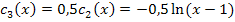
Verschiebung von 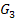um 3 nach oben

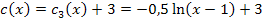
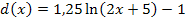
Um die Funktion auf die Form 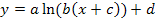zu bringen, klammern wir im Argument des ln die Zahl 2 aus.

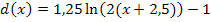
Jetzt kann man ablesen:

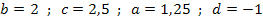
Der Graph 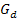der Funktion 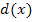entsteht deshalb durch folgende Abbildungen aus dem Graph 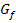der Funktion :

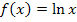  • Keine Spiegelung an der y-Achse (weil b positiv ist)
  • Stauchung entlang der x-Achse mit dem Faktor
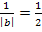
  • Verschiebung um 2,5 nach links (weil c positiv ist)
  • Keine Spiegelung an der x-Achse (weil a positiv ist)
  • Streckung entlang der y-Achse mit dem Faktor 1,25
  • Verschiebung um 1 nach unten (weil d negativ ist)

Alternativ dazu kannst du auch gleich direkt von 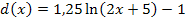, also ohne vorheriges Ausklammern der Zahl 2 im Argument des ln, dir die nötigen Abbildungen „von innen nach außen“ überlegen.

Der Graph 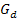von 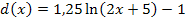ergibt sich auch folgendermaßen:

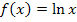
Verschiebung von 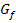um 5 nach links

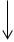
Stauchung von 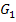entlang der x-Achse mit dem Faktor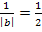

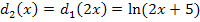
Streckung von 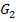entlang der y-Achse mit dem Faktor 1,25

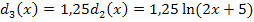
Verschiebung von 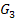um 1 nach unten

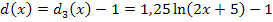
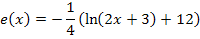
Um die Funktion auf die Form 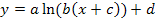zu bringen, multiplizieren wir den Faktor 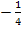mit dem Term in der Klammer, außerdem klammern wir im Argument des ln die Zahl 2 aus.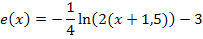

Jetzt kann man ablesen:

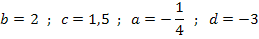
Der Graph 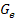der Funktion 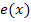entsteht somit durch folgende Abbildungen aus dem Graph 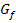der Funktion :

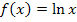  • Keine Spiegelung an der y-Achse (weil b positiv ist)
  • Stauchung entlang der x-Achse mit dem Faktor
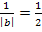
  • Verschiebung um 1,5 nach links (weil c positiv ist)
  • Spiegelung an der x-Achse (weil a negativ ist)
  • Stauchung entlang der y-Achse mit dem Faktor
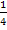
  • Verschiebung um 3 nach unten (weil d negativ ist)

Wenn man die Funktion in der angegebenen Form 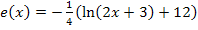stehen lassen will, kann man ihren Graph 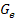auf die folgende Art und Weise aus dem Graph 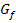der Funktion 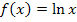herleiten.

·        Verschiebung von 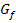um 3 nach links;das ergibt den Graph 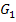der Funktion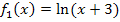

·        Stauchung von 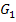entlang der x-Achse mit dem Faktor 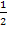;das ergibt den Graph 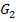der Funktion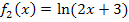

·        Verschiebung von 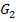um 12 nach oben;das ergibt den Graph 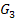der Funktion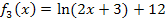

·        Stauchung von 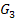entlang der y-Achse mit dem Faktor 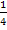;das ergibt den Graph 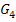der Funktion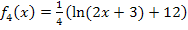

·        Spiegelung von 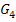an der x-Achse;das ergibt den Graph 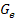der Funktion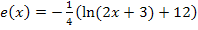

Die letzten beiden Abbildungen können von ihrer Reihenfolge auch vertauscht werden.

0
0
0
0