Das Summenzeichen und die Streifenmethode

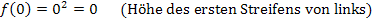
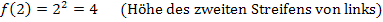
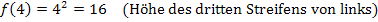
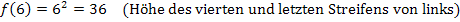
Nun können wir leicht die Untersumme 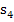berechnen, indem wir, wie schon bei der Obersumme, bei jedem Streifen „Breite mal Höhe“ rechnen und die Ergebnisse alle addieren.

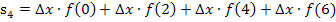
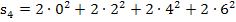
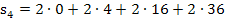
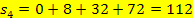
Mittelwertbildung aus Ober- und Untersumme:

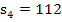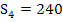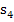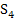Der exakte Inhalt der gesuchten Fläche A muss somit zwischen der Untersumme und der Obersumme liegen. Wir bilden noch das arithmetische Mittel, d.h. den Durchschnitt, von und . Das ergibt den zweiten Näherungswert für .

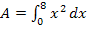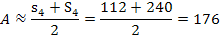
Dieser Näherungswert ist schon etwas genauer, als der, den wir vorher mit nur zwei Streifen ermittelt haben.

Allerdings sind vier Streifen noch nicht ausreichend, um wirklich einen guten Näherungswert für A zu finden. Dafür brauchen wir noch etwas mehr Streifen. Deshalb das Ganze gleich noch einmal, aber nun mit acht Streifen. (Keine Sorge! Danach ist Schluss, noch mehr Streifen werden wir nicht mehr machen. Aber danach geht es weiter mit dem allgemeinen Fall n Streifen und der oberen Grenze b. Dafür musst du das Prinzip wirklich verstanden haben. Deshalb bitte jetzt nicht gelangweilt abbrechen, sondern wirklich erst mal mit 8 Streifen selbst rechnen. Erst danach weiterlesen und deine Ergebnisse mit der gezeigten Lösung vergleichen.)

3. Näherung mit der Streifenanzahl n = 8

Näherungsweise zu berechnen: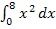

Es gilt somit:

Untere Grenze a = 0, obere Grenze b = 8 und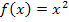

Berechnung der Obersumme :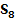

Die Streifenbreite ergibt sich aus der Intervallbreite b – a = 8 – 0 = 8 und der Anzahl n (hier n = der Streifen:

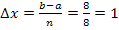
Dass sich bei 8 Streifen im Intervall von 0 bis 8 die Streifenbreite 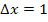ergibt, leuchtet von selbst ein. Man erkennt dies natürlich auch an der nachfolgenden Abbildung. Jeder der acht Streifen hat die Breite .

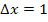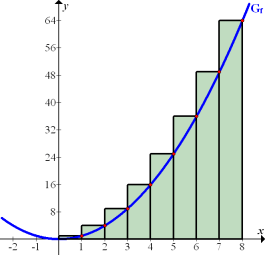
Abb. 6:Zur Berechnung der Obersumme 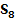im Intervall 0 bis 8 mit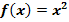

Die Streifenhöhe ergibt sich jeweils aus der y-Koordinate des höchsten Kurvenpunktes innerhalb der einzelnen Streifen. (In Abb. 6 rot markierte Punkte) Diese Punkte liegen wie immer bei Obersummen streng monoton steigenden Graphen  in der rechten, oberen Ecke des entsprechenden Streifens. Ihre y-Koordinaten, d.h. die Streifenhöhen, berechnet man hier jeweils durch Einsetzen der x-Koordinaten 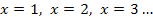bis 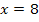in die Funktionsgleichung 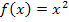. Die Streifenhöhen ergeben sich demnach au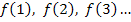s bis .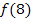

Nun lässt sich die Obersumme 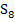berechnen, indem man bei jedem der acht Streifen „Breite mal Höhe“ rechnet und alle acht Ergebnisse addiert.

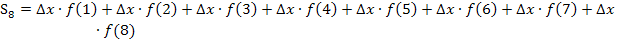
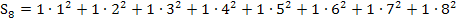
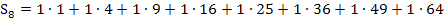
Berechnung der Untersumme :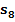

---