Uneigentliche Integrale
Da sowohl der Zähler als auch der Nenner immer positiv ist, egal was für x eingesetzt wird, ist auch der Bruch immer positiv.

Dir ist nicht klar, warum 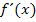 immer positiv ist?
immer positiv ist?
Ok, dann noch einmal ganz langsam. Als erstes muss du wissen, dass 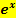 grundsätzlich positiv ist;die e-Funktion verläuft schließlich immer oberhalb der x-Achse. Daher ist der Zähler der Ableitung auf jeden Fall positiv. Der Nenner
grundsätzlich positiv ist;die e-Funktion verläuft schließlich immer oberhalb der x-Achse. Daher ist der Zähler der Ableitung auf jeden Fall positiv. Der Nenner 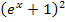 ist ebenfalls positiv, da zu dem ohnehin schon positiven Ausdruck
ist ebenfalls positiv, da zu dem ohnehin schon positiven Ausdruck 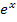 auch noch die Zahl 1 dazu gezählt und das Ganze quadriert wird. Wenn
auch noch die Zahl 1 dazu gezählt und das Ganze quadriert wird. Wenn 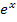 bereits positiv ist, ist es
bereits positiv ist, ist es 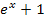 erst recht. Das Quadrat davon ist dann folglich ebenfalls größer als Null. Der gesamte Bruch ist somit auch größer Null. (Etwas Positives durch etwas Positives geteilt, bleibt schließlich positiv.)
erst recht. Das Quadrat davon ist dann folglich ebenfalls größer als Null. Der gesamte Bruch ist somit auch größer Null. (Etwas Positives durch etwas Positives geteilt, bleibt schließlich positiv.)
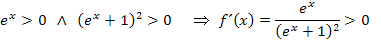
Die Ableitung ist somit für beliebige Werte von x immer größer Null. Wir folgern daraus:Die Funktion 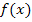 besitzt keine Extrema, da
besitzt keine Extrema, da 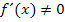 ist. Wegen
ist. Wegen 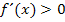 ist der Graph streng monoton steigend innerhalb der gesamten Definitionsmenge.
ist der Graph streng monoton steigend innerhalb der gesamten Definitionsmenge.
Zu 2c.)
Mit Hilfe der beiden Asymptoten 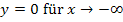 und
und 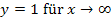 lässt sich der Graph skizzieren.
lässt sich der Graph skizzieren.
Außerdem berechnen wir noch schnell den Schnittpunkt von 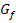 mit der y-Achse. Das geht schnell und erleichtert uns das Zeichnen. Bekanntlich hat die y-Achse die Gleichung x = 0. Um den Schnittpunkt von
mit der y-Achse. Das geht schnell und erleichtert uns das Zeichnen. Bekanntlich hat die y-Achse die Gleichung x = 0. Um den Schnittpunkt von 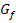 mit der y-Achse zu berechnen, müssen wir nur für x die Zahl 0 in die Funktionsgleichung
mit der y-Achse zu berechnen, müssen wir nur für x die Zahl 0 in die Funktionsgleichung 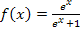 einsetzen.
einsetzen.
Berechnung des Schnittpunkts mit der y-Achse:
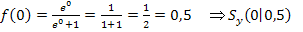
Nun lässt sich der Graph  leicht skizzieren.
leicht skizzieren.
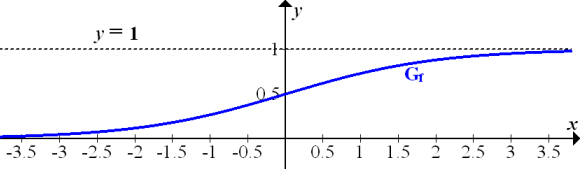
Abb.:Graph  der Funktion
der Funktion 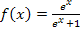 und die Gerade y =1
und die Gerade y =1
Zu 2d.)
Jetzt wird es interessant, denn nun kommt die Teilaufgabe, die im Prinzip ein uneigentliches Integral enthält. Gesucht ist diejenige Fläche, die im II. Quadranten zwischen dem Funktionsgraph 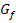 , der senkrechten Gerade x = u und den Koordinatenachsen liegt. Es gilt
, der senkrechten Gerade x = u und den Koordinatenachsen liegt. Es gilt 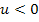 , daher handelt es sich bei der Gerade x = u um eine links von der y-Achse liegende, senkrechte Gerade.
, daher handelt es sich bei der Gerade x = u um eine links von der y-Achse liegende, senkrechte Gerade.
Damit du dir das Ganze besser vorstellen kannst, solltest du dir einfach eine beliebige, aber auf jeden Fall negative Zahl für u denken, beispielsweise u = – 3, und diese Zahl bei x = u für u einsetzen. Du erhältst so die Gerade x = – 3 als konkretes Beispiel für x = u. Jetzt zeichnest du die Gerade x = – 3 als konkretes Beispiel für x = u in die Zeichnung ein, die bereits den Funktionsgraphen enthält. Dann markierst du die Fläche, die im II. Quadranten zwischen dem Funktionsgraphen 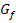 , der senkrechten Geraden x = – 3 und den Koordinatenachsen liegt.
, der senkrechten Geraden x = – 3 und den Koordinatenachsen liegt.

