1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen

5. Bsp.:Berechne die folgenden Integrale!

a.)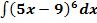

b.)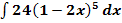

c.)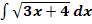

d.)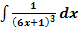

e.)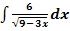

f.)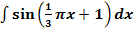

g.)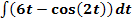

h.)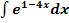

i.)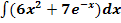

j.)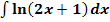

Lösung:

Zu 5a.)

Berechnet werden soll das Integral 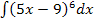. Es handelt sich offensichtlich um das Integral einer linear transformierten Funktion. In die Grundfunktion 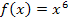ist die lineare Funktion 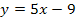eingesetzt worden. So entstand die Funktion 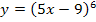, die wir integrieren sollen. Wir verwenden die Formel: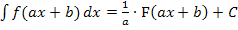

Der Koeffizient a (Zahl vor dem x) ist hier 5. Wenn man das Integral 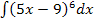ausrechnet, muss laut der Formel mit begonnen werden, hier also mit .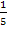

Dann ermitteln wir eine Stammfunktion F der Grundfunktion .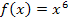

Dazu bedienen wir uns der Integrationsregel 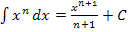. (Diese Regel steht bei den Grundintegralen in deiner Formelsammlung bzw. Merkhilfe.)

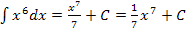
Nun kennen wir die Stammfunktion 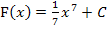der Grundfunktion .

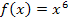Bei F ersetzen wir nun x durch den Ausdruck .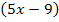

So ergibt sich .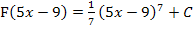

Das multiplizieren wir nun mit dem Faktor 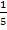, mit dem wir begonnen haben das gesuchte Integral 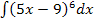zu berechnen.

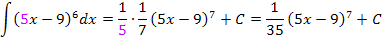
Und schon sind wir fertig.

Hinweis:Die Konstante C muss nicht mit 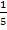multipliziert werden.

Du willst wissen, warum das so ist? Ok, dann machen wir das ´mal ganz ausführlich. Bei der Integration bezeichnen wir die Integrationskonstante allerdings zuerst einmal mit C* und noch nicht mit C.

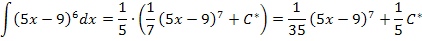
Nun setzen wir 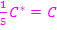. Es ergibt sich:

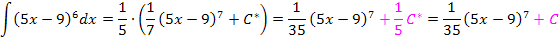
Die Integrationskonstante ist sowieso unbekannt. Deshalb ist es egal, ob man C mit 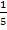multipliziert oder nicht. Du kannst also entweder „+ C “ oder auch „+ 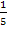C “ schreiben. Beides ist korrekt, aber „+ C “  ist doch etwas schöner.

Zu 5b.)

Zu berechnen ist das Integral 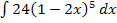. Es handelt sich wieder um eine linear transformierte Funktion. Damit du leichter erkennen kannst, was hier dem Koeffizienten a entspricht, vertauschen wir die Reihenfolge innerhalb der Klammer.

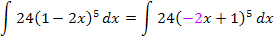
Nun ist klar, dass a hier der Zahl – 2 entspricht.

Laut der Formel 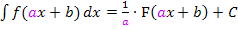müssen wir bei der Integration mit 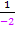, also mit 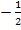beginnen. Die Zahl 24 im Integral 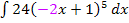ist eine multiplikative Konstante (d.h. eine Zahl, mit der multipliziert wird);solche Zahlen bleiben beim Integrieren (genauso wie beim Ableiten) einfach stehen. Wir schreiben sie einfach ab.

Die Grundfunktion ist hier .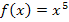

Aus 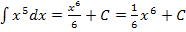ergibt sich die Stammfunktion F(x) der Grundfunktion 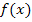. Bei F ersetzen wir x noch durch den Ausdruck 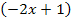. Wer mag, kann zum Schluss die Reihenfolge innerhalb der Klammer wieder umdrehen und 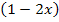schreiben.

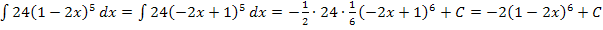
Zu 5c.

---