2a. Partielle Integration
Die partielle Integration ist eine „Art Produktregel zum Integrieren“;man verwendet sie bei der Berechnung von Integralen der Form 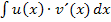 . (Bitte wundere dich nicht, warum der zweite Faktor des zu integrierenden Produkts hier
. (Bitte wundere dich nicht, warum der zweite Faktor des zu integrierenden Produkts hier 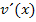 und nicht
und nicht 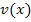 heißt. Das wird gleich noch erklärt.)
heißt. Das wird gleich noch erklärt.)
Der Name „partielle Integration“ = „teilweise Integration“ kommt daher, dass zwar ein Teil der Funktion sofort integriert wird, aber gleichzeitig ein neues Integral entsteht, das man erst in einem zweiten Schritt lösen muss. Damit dir klar wird, wie das gemeint ist, schauen wir uns doch gleich die Formel für die partielle Integration an.
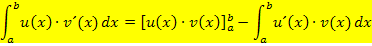
Hinweis:Mit Hilfe der partiellen Integration können nicht nur bestimmte Integrale, sondern auch unbestimmte Integrale berechnet werden. Dann entfallen einfach die Integrationsgrenzen a und b. Du musst dann allerdings, wie bei allen unbestimmten Integralen, noch „+ C “ beim Ergebnis dazu schreiben.
Es geht bei der partiellen Integration also um die Integration eines Produkts, das in beiden Faktoren die Variable x enthält. Der eine Faktor des zu integrierenden Produkts wird mit 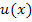 bezeichnet, der andere mit
bezeichnet, der andere mit 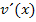 . In der Formel für die partielle Integration kommen neben
. In der Formel für die partielle Integration kommen neben 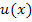 und
und 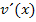 auch
auch 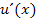 und
und 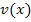 vor.
vor. 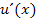 erhält man natürlich, indem man den Faktor
erhält man natürlich, indem man den Faktor 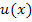 ableitet.
ableitet. 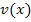 erhält man, wenn man den Faktor
erhält man, wenn man den Faktor 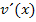 integriert. Der Faktor
integriert. Der Faktor 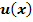 muss deshalb abgeleitet, der andere Faktor
muss deshalb abgeleitet, der andere Faktor 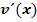 dagegen integriert werden.
dagegen integriert werden.
In anderen Worten:Du nimmst den einen Faktor 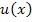 und bildest am besten in einer Nebenrechnung die Ableitung
und bildest am besten in einer Nebenrechnung die Ableitung 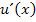 . Außerdem nimmst du den anderen Faktor
. Außerdem nimmst du den anderen Faktor 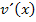 und berechnest auch in einer Nebenrechnung
und berechnest auch in einer Nebenrechnung 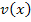 , d.h. du integrierst
, d.h. du integrierst 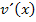 . Danach setzt du alles in die Formel für die partielle Integration ein.
. Danach setzt du alles in die Formel für die partielle Integration ein.
Der vordere Teil des Ergebnisses 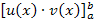 ist dann bereits integriert, aber der hintere Teil
ist dann bereits integriert, aber der hintere Teil 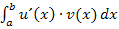 muss später integriert, also in einem weiteren Rechenschritt gelöst werden. Dieses neu entstandene Integral muss natürlich leichter auszurechnen sein als das ursprüngliche;sonst macht die Rechnung keinen Sinn. Genau das ist das Problem.
muss später integriert, also in einem weiteren Rechenschritt gelöst werden. Dieses neu entstandene Integral muss natürlich leichter auszurechnen sein als das ursprüngliche;sonst macht die Rechnung keinen Sinn. Genau das ist das Problem.

