2a. Partielle Integration
Man muss selbst erkennen, welchen Faktor des Produkts man als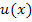 
und welchen man als 
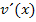wählt, damit das neue Integral einfacher wird als das ursprüngliche.
Woran erkennst du, was 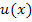und entsprechend 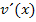in einem konkreten Fall ist? Das hängt vom Typ des Integrals ab. Es gibt drei unterschiedliche Typen bei der partiellen Integration:
1. Typ „Abräumen“
2. Typ „Faktor 1“
3. Typ „Phönix“
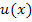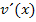Diese drei Typen werden im Folgenden einzeln besprochen. Dabei wird auch erklärt, wie jeweils und festzulegen sind.
1. Typ „Abräumen“
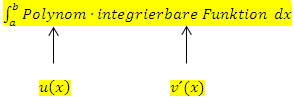
Es liegt ein Integral der Form 
vor. (Das Polynom sollte dabei nicht höher als dritten Grades sein, weil man sonst zu lange rechnen müsste. Erklärung folgt noch.)
Das Polynom entspricht dabei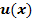 
, es muss also abgeleitet werden. Der andere Faktor 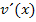muss integriert werden. Daher muss 
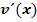eine Funktion sein, die sich integrieren lässt, wie zum Beispiel 
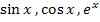oder eine lineartransformierte Funktion wie z. B. 
.
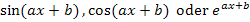Am besten schauen wir uns gleich ein konkretes Beispiel dafür an.
7. Bsp.:Berechne den Wert des folgenden bestimmten Integrals!
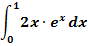
Lösung:
Es handelt sich um das Integral eines Produkts, das in beiden Faktoren die Variable x enthält.
Vorsicht:Die Faktoren dürfen keinesfalls einzeln integriert werden!
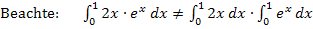
Um das Integral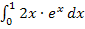 
zu berechnen, muss man die partielle Integration Typ „Abräumen“ verwenden. Anders geht es nicht!
Der Faktor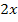 
entspricht dabei dem Polynom;wir bezeichnen es mit 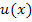, kurz u.
Der zweite Faktor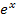 
ist eine leicht integrierbare Funktion; 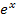entspricht hier somit 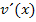, kurz v´.
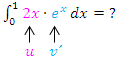
In einer Nebenrechnung müssen wir vorweg u´ und v bilden.
Das kannst du bestimmt auch alleine. Zu deiner Kontrolle hier die Zwischenergebnisse:
Nun setzen wir alles in die Formel der partiellen Integration ein.
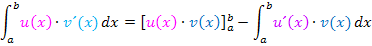
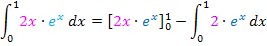
Das Polynom wurde durch das Ableiten praktisch „abgeräumt“;die Variable x kommt im neu entstandenen Integral nur noch im Exponenten von 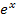vor. Daher auch die Bezeichnung „Abräumen“. Das neue Integral ist leichter zu berechnen als das ursprüngliche, da es sich beim neuen Integranden nicht mehr um ein Produkt handelt, das in beiden Faktoren die Variable x enthält.
Das neue Integral lässt sich leicht lösen. Der Faktor 2 bleibt beim Integrieren einfach stehen und 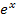ergibt integriert wieder .
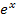Beim vorderen Teil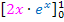 
müssen natürlich noch die Integrationsgrenzen eingesetzt werden. Denk´daran:Obere Grenze minus untere!
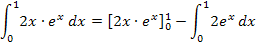
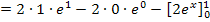
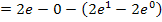
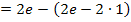
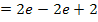
In diesem Beispiel ist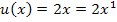 
ein Polynom ersten Grades.
