1. Flächenberechnungenmit Hilfe von Integralen
Die Funktion f ist eine quadratische Funktion;ihr Graph ist also eine Parabel. Entscheidend ist, dass die Parabel nach oben geöffnet ist, was man daran erkennt, dass die Zahl vor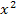 
positiv ist. Des Weiteren lässt sich am Funktionsterm direkt ablesen:Die Parabel ist breiter als die Normalparabel und hat den Scheitel S(0|1). Ausführlichere Erklärungen dazu im Kapitel:Quadratische Funktionen (Parabeln)
Die Funktion g ist eine lineare Funktion, also eine Funktion der Form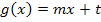 
;ihr Graph ist eine Gerade. Die Gerade schneidet die y-Achse bei 1 und hat die Steigung -1, sie fällt also. Mehr zum Thema „Geraden“ im Kapitel:Lineare Funktionen (Geraden)
Wir wissen, dass die Gerade die Parabel bei x = -4 und x = 0 schneidet. Weil die Parabel nach oben geöffnet ist, muss die Parabel die Fläche unten begrenzen und die Gerade entsprechend oben. Im Bereich der Fläche liegt also die Gerade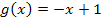 
oberhalb von der Parabel 
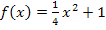. Vergleiche Abbildung!
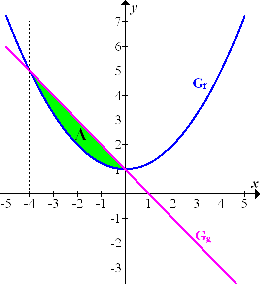
Abb.:Die Graphen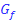 
und 
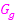der Funktionen 
schließen die Fläche A ein.
Wir müssen von der oberen Funktion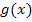 
die untere Funktion 
abziehen und davon das Integral berechnen. Weil wir außerdem von der kleineren Grenze -4 zur größeren Grenze 0 integrieren, brauchen wir keinen Betrag. Wir müssen demnach das folgende Integral berechnen, um den Inhalt der in der Abbildung grün markierten Fläche zu ermitteln:
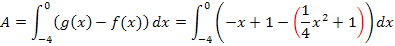
Vorsicht:Nicht die Klammer um die Funktion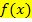 
vergessen! Das Minus, das vor dieser Funktion steht, muss sich nämlich auf die gesamte Funktionsgleichung von beziehen. Statt der Klammer kannst du natürlich auch alle Vorzeichen bei umdrehen. (Wie du weißt, dreht ein Minus vor der Klammer alle Vorzeichen des Ausdrucks in der Klammer letztendlich um.)
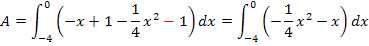
Nun bilden wir mit der Integrationsregel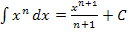 
eine Stammfunktion und setzen danach die Grenzen ein.
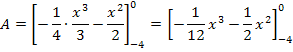
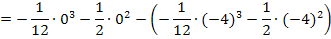
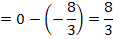
Die Fläche zwischen den beiden Funktionen 
hat somit einen Inhalt von 
FE.
2. Methode:Integral des Terms, der bei der nach Null aufgelösten Gleichung aus der Schnittpunktberechnung auf der linken Seite steht, mit Betrag berechnen
Die Grenzen haben wir oben berechnet:Die untere Grenze ist -4 und die obere Grenze 0.
Bei der Berechnung der Grenzen / Schnittpunkte haben wir folgende Gleichung gelöst:
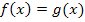
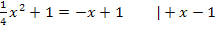
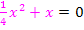
Die Gleichung ist nach Null umgestellt. Wir können nun einfach die linke Seite der Gleichung nehmen und davon den Betrag des Integrals berechnen. Das ergibt die gesuchte Fläche zwischen den beiden Funktionen .
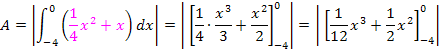
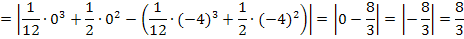
Du siehst, dass wieder das gleiche Ergebnis herauskommt wie schon oben bei der 1. Methode. Allerdings ist es nur dem Betrag zu verdanken, dass das Vorzeichen des Ergebnisses wirklich positiv ist. Deshalb ist bei dieser Methode der Betrag zwingend notwendig!
