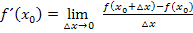Delta-x-Methode
Daher gilt:
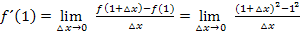
Jetzt muss der Zähler vereinfacht werden. Dazu benutzen wir die erste binomische Formel 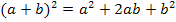 , um die Klammer zu quadrieren:
, um die Klammer zu quadrieren:
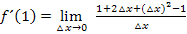
Die Zahlen 1 und -1 im Zähler heben sich weg. Das müssen sie auch unbedingt, weil sie kein  enthalten. Es muss nämlich grundsätzlich alles wegfallen, was kein
enthalten. Es muss nämlich grundsätzlich alles wegfallen, was kein  enthält. (Sonst könnte man nachher nämlich
enthält. (Sonst könnte man nachher nämlich  nicht ausklammern. Vergleiche unten!)
nicht ausklammern. Vergleiche unten!)
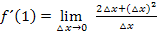
Wir klammern jetzt im Zähler  aus, das ergibt dann:
aus, das ergibt dann:
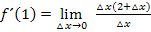
Nun kürzen wir △x weg:
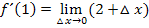
Da jetzt △x nicht mehr im Nenner steht, kann nun der Grenzwert berechnet werden. Man setzt dazu △x jetzt wirklich gleich Null. Dadurch wird aus der Sekantensteigung genau die Tangentensteigung.
Das Gleichnullsetzen von △x klappt nun auch, weil △x nach dem Kürzen nicht mehr im Nenner steht und somit der Nenner nicht mehr gleich Null wird, wenn man △x gleich Null setzt. Vorher hätten wir △x nicht gleich Null setzen können, weil dann eben der Nenner Null ergeben hätte und die Division durch Null bekanntlich nicht definiert ist.
 Wir rechnen den Limes aus, indem wir für △x die Zahl Null einsetzen:
Wir rechnen den Limes aus, indem wir für △x die Zahl Null einsetzen:
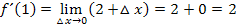
Die Steigung der Tangente an die Funktion 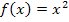 im Punkt
im Punkt 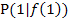 ist daher genau 2.
ist daher genau 2.
Hier noch einmal das Wichtigste allgemein zusammengefasst:
Man leitet die Tangentensteigung 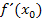 einer Funktion
einer Funktion 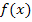 an einer bestimmten Stelle
an einer bestimmten Stelle 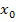 auf folgende Art und Weise aus der Sekantensteigung her.
auf folgende Art und Weise aus der Sekantensteigung her.
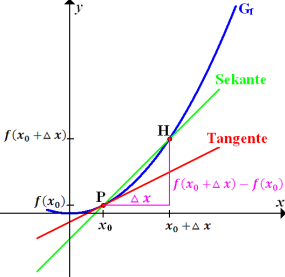
Der Hilfspunkt 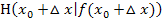 wird in Gedanken beliebig nah an den festen Punkt
wird in Gedanken beliebig nah an den festen Punkt 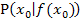 herangeschoben;man lässt
herangeschoben;man lässt  also gegen Null gehen. Dadurch kommt man von der Sekantensteigung
also gegen Null gehen. Dadurch kommt man von der Sekantensteigung 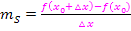 zur gesuchten Tangentensteigung:
zur gesuchten Tangentensteigung:
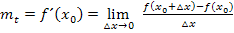
Wir nennen dieses Verfahren zur Berechnung der Tangentensteigung auf dieser website die „Delta-x-Methode“. Das ist aber keine offizielle Bezeichnung. Im Allgemeinen wird dies einfach als Berechnung der Tangentensteigung mit dem Differenzialquotienten bezeichnet.
Hier noch einmal die wichtigsten Schritte, wie du an einer bestimmten Stelle 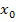 die Tangentensteigung, d.h. die Ableitung
die Tangentensteigung, d.h. die Ableitung 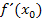 einer Funktion
einer Funktion 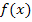 , mit der „Delta-x-Methode“ berechnen kannst.
, mit der „Delta-x-Methode“ berechnen kannst.
Geg.: 
Anleitung zur Berechnung der Tangentensteigung im Punkt Ansatz: · Für · Zähler des Ausdrucks so weit möglich vereinfachen, d.h. Klammern ausrechnen, evtl. binomische Formelnanwenden und zusammenfassen (Es muss im Zähler alles wegfallen, was kein · Im Zähler · Mit · Grenzwert berechnen, indem du für Das Ergebnis ist eine konkrete Zahl, welche die Steigung der Funktion / der Tangente im Kurvenpunkt |
Wie oben schon erwähnt, heißt dies auch „lokales Differenzieren“.

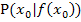 mit dem Differenzialquotienten nach der „Delta-x-Methode“:
mit dem Differenzialquotienten nach der „Delta-x-Methode“: