Variante 3
Und gleich noch ein interessantes Beispiel:
5. Bsp.:
Gegeben ist die Funktion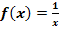 
mit ihrer maximalen Definitionsmenge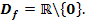 
a.) Berechne die Ableitungsfunktion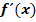 
mit Hilfe des Differenzialquotienten!
b.) Ermittle die Gleichung der Tangente an den Graph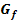 
im Kurvenpunkt 
!
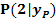Lösung:
Zu 5a.)
Es soll die Ableitungsfunktion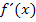 
mit Hilfe des Differenzialquotienten ermittelt werden, Dazu müssen wir vorweg die Ableitung 
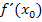an der Stelle 
bilden und danach rein formal durch x ersetzen.
Allgemeiner Ansatz für den Differenzialquotienten:
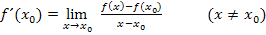
Versuche es doch erst ´mal alleine, den Differenzialquotienten für die Funktion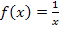 
zu bilden, bevor du weiter liest!
Hast du es inzwischen selbst probiert? Dann müsstest du eigentlich zu folgendem Ergebnis gekommen sein:
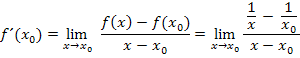
Nun muss das Ganze aber noch so umgeformt werden, dass sich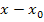 
wieder herauskürzen lässt. Als erstes bringen wir die beiden Brüche im Zähler des Differenzialquotienten auf einen gemeinsamen Nenner. Der Hauptnenner ist natürlich 
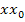, deshalb muss der erste Bruch mit und der zweite Bruch mit x erweitert werden.
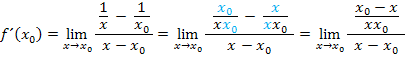
Nun wollen wir den Doppelbruch beseitigen. Dazu stellen wir uns den Hauptbruchstrich (den längsten Bruchstrich) als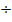 
vor. Statt des Ausdrucks 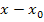im Nenner kann man sich im Nenner auch den Bruch 
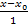denken. Da man durch einen Bruch dividiert, indem man mit dem Kehrwert multipliziert, kann an Stelle der Division durch den Bruch 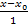auch eine Multiplikation mit dem Kehrbruch 
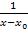vorgenommen werden. Das geht dann folgendermaßen:
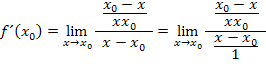
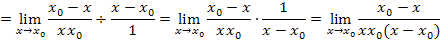
Damit sich 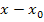wegkürzen lässt, muss im Zähler ein Minus, d.h. eigentlich die Zahl -1, ausgeklammert werden.
Warum? Ganz einfach:Damit der Grenzwert berechnet werden kann, d.h. letztendlich für x eingesetzt werden kann, muss 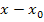aus dem Nenner beseitigt/gekürzt werden. (Ansonsten würde sich im Nenner Null ergeben, wenn man für x einsetzt.) In der vorliegenden Form ist das Kürzen von 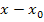noch nicht möglich, da momentan im Zähler der Ausdruck 
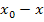steht, also die Reihenfolge von x und noch genau umgekehrt ist. Es hilft der schon erwähnte Trick, im Zähler ein Minus auszuklammern. An sich kann entweder bei dem Ausdruck 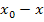im Zähler oder bei 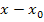im Nenner der Faktor -1, also praktisch ein Minuszeichen, ausgeklammert werden.
