Das bestimmte und das unbestimmte Integral
Manche bestimmten Integrale lassen sich berechnen, obwohl man keine Stammfunktion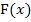 
zu 
finden kann. Das funktioniert allerdings nur dann, wenn das Integral einer Fläche entspricht, deren Inhalt sich elementargeometrisch berechnen lässt (z. B. mit der Formel für den Flächeninhalt eines Rechtecks, Trapezes, Dreiecks oder Kreises bzw. zusammengesetzt aus diesen Formeln). Im nächsten Beispiel haben wir so einen Fall.
7.Bsp.:
Gegeben ist die Funktion 
mit ihrer maximalen Definitionsmenge 
. Zeichne den Graph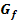 
der Funktion 
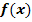und ermittle den Wert des Integrals 
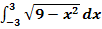! (Überlege dir dazu, was das gesuchte Integral anschaulich bedeutet.)
Lösung:
Mit Hilfe einer Wertetabelle kannst du den Graph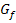 
der Funktion 
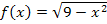bestimmt alleine zeichnen. Was vermutest du über den Graph ?
Scheinbar beschreibt die Funktion einen Halbkreis mit dem Ursprung des Koordinatensystems als Mittelpunkt und dem Radius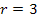 
.
Diese Vermutung lässt sich folgendermaßen bestätigen:
Wir wählen einen beliebigen Punkt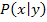 
auf dem Halbkreis um 
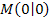mit Radius 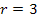und zeichnen den Punkt und das Dreieck in das Koordinatensystem, welches der Punkt mit seiner Abszisse (x-Koordinate) und seiner Ordinate (y-Koordinate) bildet. Vergleiche Skizze!
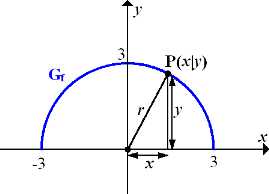
Das eingezeichnete Dreieck ist rechtwinklig, da die Abszisse x und die Ordinate y senkrecht zueinander liegen. Der Radius r ist die Hypotenuse des rechtwinkligen Dreiecks, weil r gegenüber des rechten Winkels liegt.
Zur Erinnerung:In jedem rechtwinkligen Dreieck ABC mit c als Hypotenuse gilt der Satz des Pythagoras: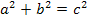 
Für jeden Punkt 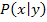, der auf einem Halbkreis um 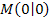mit Radius r liegt, lässt sich mit Hilfe des Satzes von Pythagoras folgende Gleichung aufstellen:
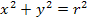
Mit 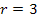ergibt sich:
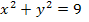
Wenn man nach y auflöst, erhält man:
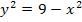
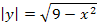
Die Gleichung 
beschreibt den oberhalb der x-Achse liegenden Halbkreis. Die Gleichung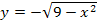 
würde den unterhalb der x-Achse liegenden Halbkreis beschreiben. Wir interessieren uns nur für den oberhalb der x-Achse liegenden Halbkreis. Offensichtlich hat jeder Punkt des oberen Halbkreises eine positive y-Koordinate oder y = 0.
Daher gilt in unserem Fall zwangsläufig die Gleichung und dies ist ja genau die Gleichung unserer Funktion 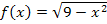. ist schließlich nur eine andere Schreibweise für y. Damit ist klar, dass der Graph 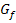tatsächlich ein Halbkreis um 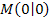mit Radius 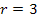ist.
Das gesuchte Integral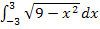 
entspricht offensichtlich der gesamten Fläche des Halbkreises um 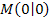mit Radius 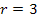. Siehe blau unterlegte Fläche!
